反函数和原函数的关系主要体现在以下几个方面定义域与值域的互换反函数的定义域是原来函数的值域反函数的值域是原来函数的定义域函数性质函数的反函数，本身也是一个函数这意味着反函数同样具有定义域值域和对应法则偶函数必无反函数这是因为偶函数对于定义域内的任意x，都有fx = fx，即存在。

反函数与原函数存在以下区别1定义域与值域原函数的定义域和值域分别是反函数的值域和定义域2函数关系任何一个原函数与其反函数互为反函数，即原函数与其反函数关系是相互唯一的3图像关系原函数和它的反函数图象关于直线y=x对称4单调性偶函数没有反函数单调函数必有反函数。

反函数与原函数的关系反函数是原函数的一种映射关系，即对于原函数的输入值，反函数可以将其映射到对应的输出值这种关系具有对称性，即原函数与反函数在定义域和值域上是相互对应的也就是说，如果有一个函数f，其定义域为x的取值范围，值域为f的取值范围，那么它的反函数g的定义域就是f的值域，值域则是x的取值范。

1原函数值域就是反函数定义域，而原函数定义域则是反函数值域，它们在各自的定义域上单调性也一样2对于函数而言，它的反函数本也是一个函数，根据反函数的定义，可以得出原函数是其反函数的反函数，所以对于函数而言，原函数和反函数互相称为反函数。

反函数与原函数的关系主要体现在它们的单调性和导数关系上单调性一致如果原函数f在定义域D上严格单调递增，那么其反函数f^1在f上也严格单调递增同样地，如果原函数f在定义域D上严格单调递减，那么其反函数f^1在f上也严格单调递减导数互为倒数在原函数f和反函数f^1的可导点上，它们的导数。

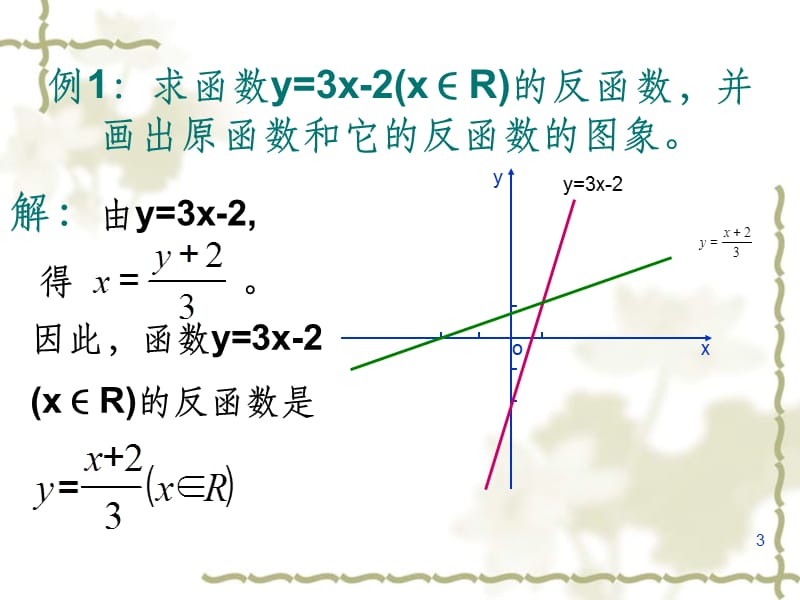
关系是关于y=x对称理由设 x，y在baiy=fx上于是 x=f1y即 Y，x在y=fx的反函数上易知 x，y ，y，x关于原点对称而 x，y ，y，x有分别zhi在原函数与反函数上所以整个图像是关于y=x对称的。

反函数与原函数的关系反函数的定义域与值域分别是原函数的值域与定义域函数的反函数，本身也是一个函数，由反函数的定义，原函数也是其反函数的反函数，故函数的原函数与反函数互称为反函数偶函数必无反函数奇函数如果有反函数，其反函数也是奇函数原函数与其反函数在他们各自的定义域上单调。 2025年天天彩免费大全

原函数和反函数是互为反函数的关系具体来说，如果一个函数的定义域和值域分别是另一个函数的值域和定义域，那么这两个函数互为反函数在数学中，反函数是一个重要的概念，它可以将一个函数映射到另一个函数原函数和反函数的关系可以用来解决一些复杂的问题，也可以用来理解函数的性质和行为首先。